
|
ШАХМАТЫ ОНЛАЙН. Игра с реальным оппонентом в классические и нестандартные виды шахмат. Турниры, матчи. Бесплатно, без ограничений. |
|||
|
22:59:11, 23.02.2026
|
Главная Регистрация Восстановить пароль Форум Помощь | |||
| Авторизация |

| Статистика портала |
|
Пользователей: всего - 20972 на сайте - 2 Гостей на сайте: 280 Команд BugHouse: всего - 280 на сайте - 1 Партий: всего - 401918 завершенных - 401407 Турниров: активных - 77 завершенных - 15623 Расстановок: 29751 |
Шахматы Мир шахмат Правила шахмат К Администрации Беседка Поздравления Спорт Дискуссии Правила форума Шахматы -> Рейтинг Эло для шахматистов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15:35:46 16.05.12 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
admin Сообщений:72 |
РџРѕРґ рейтингами Рло обычно подразумевают рейтинги Р¤РДЕ, однако существуют Рё РґСЂСѓРіРёРµ рейтинги: рейтинг шахматной федерации РЎРЁРђ, рейтинг Клуба интернет-шахмат (Internet Chess Club), рейтинг Профессиональной шахматной ассоциации (РџРЁРђ). Каждая система рейтингов имеет СЃРІРѕРё особенности Рё РЅРµ следует РІ точности первоначальным предположениям Рло.
Р’ шахматах рейтинг Рло вычисляется РїРѕ результатам РёРіСЂ шахматистов РґСЂСѓРі СЃ РґСЂСѓРіРѕРј. Система рейтингов Рло делит шахматистов РЅР° девять классов: высший класс начинается СЃ рейтинга 2600, низший класс соответствует рейтингу 1200 Рё ниже.
Примерное соответствие рейтингов Рло Рё шахматных званий Рё разрядов:
Р’ системе рейтингов Рло принято, что переход РѕС‚ РѕРґРЅРѕРіРѕ класса РёРіСЂС‹ Рє следующему РїСЂРѕРёСЃС…РѕРґРёС‚ примерно через 200 пунктов рейтинга. Если различие между РґРІСѓРјСЏ игроками составляет 200 пунктов, то сильнейший РёРіСЂРѕРє набирает РІ среднем около 0,76 очка Р·Р° РёРіСЂСѓ, если различие составляет 400 пунктов, то это среднее примерно равно 0,91. Различие РІ 600 пунктов означает, что сильнейший РёРіСЂРѕРє выигрывает «почти» всегда (РІ среднем около 0,97 очка Р·Р° РёРіСЂСѓ). Если рейтинги РѕР±РѕРёС… РёРіСЂРѕРєРѕРІ равны, вероятность победы РѕРґРЅРѕРіРѕ РёР· РЅРёС… равна вероятности победы РґСЂСѓРіРѕРіРѕ РёР· РЅРёС… (что равносильно среднему количеству 0,5 очков Р·Р° РёРіСЂСѓ). Рти вероятности, конечно, РЅРµ учитывают резко изменившуюся спортивную форму РёРіСЂРѕРєР° РІ конкретный момент. Напротив, если сила РёРіСЂРѕРєР° изменяется относительно медленно (РІ то время как РёРіСЂРѕРє РїСЂРѕРІРѕРґРёС‚ статистически достаточно большое количество РёРіСЂ, учитываемых для изменения рейтинга), то рейтинг постоянно подстраивается РїРѕРґ изменения силы РёРіСЂРѕРєР°. Чем стабильнее играет шахматист, тем точнее можно оценить его рейтинг. Наиболее точно рейтинг можно получить РЅР° РѕСЃРЅРѕРІРµ турниров, РІ которых играют примерно равные РїРѕ силам РёРіСЂРѕРєРё.
Р’ РѕСЃРЅРѕРІРµ системы рейтингов Рло лежит допущение, что сила каждого шахматиста может быть представлена как вероятностная переменная, подчиняющаяся нормальному распределению. Расчёт рейтинга конкретного РёРіСЂРѕРєР° РїРѕ результатам какого-либо турнира основан РЅР° сравнении количества набранных РёРј очков СЃ ожидаемым, предсказанным РЅР° РѕСЃРЅРѕРІРµ его рейтинга, количеством очков. Если РїРѕ итогам турнира количество набранных очков оказывается больше, чем предсказанное значение, то рейтинг данного РёРіСЂРѕРєР° возрастает. Если РїРѕ итогам турнира количество набранных очков оказывается меньше, чем предсказанное значение, то рейтинг данного РёРіСЂРѕРєР° уменьшается.
Шахматист, добившийся высокого рейтинга Рло (например, РІ Рнтернете), РЅРµ может РЅР° этом основании претендовать РЅР° соответствующее шахматное звание или разряд, поскольку эти разряды Рё звания присуждаются РЅР° основании выполнения определённых несвязанных СЃ рейтингом РЅРѕСЂРј (участие РІ определённых турнирах Рё РґСЂ.). Звания Гроссмейстер (международный гроссмейстер) Рё Международный мастер присуждаются Международной Шахматной Федерацией (Р¤РДЕ).
Вычисление рейтинга РлоВычисляется математическое ожидание количества очков, которое наберёт РёРіСЂРѕРє A РІ партии СЃ B (РѕРЅРѕ равно СЃСѓРјРјРµ вероятности выигрыша РёРіСЂРѕРєР° A Рё половины вероятности ничьей):  , ,РіРґРµ:
Новый рейтинг игрока A рассчитывается по формуле: 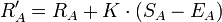 , ,где:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общий чат |
|
19:52-Evgen1909: Была бы моя воля-утопил бы это"водоплавающее"!!!
 19:31-Raido: Водоплавающие птицы тоже есть... А вообще кое-что иное тоже плавает... 19:08-Evgen1909: Только один Михаил его"пожалел и приласкал"... Никому оказался не нужен! 19:03-Evgen1909: https://youtu.be/kIAbYbB4Qhc?si=68GsSh_GLV6c15JN 19:02-Evgen1909: Пингвин-какая никакая птица... 19:01-Evgen1909: Цитата(Raido):"Пингвин уплыл? 18:47-Raido: Пингвин уплыл?.. 18:47-Raido:   18:43-foxter: Друзья! сайт crazy-chess.ru полностью восстановлен и полностью дублирует этот сайт. я думаю, через месяц мы полностью туда перейдем. пока не точно, но 12:04-sasha1960: С Праздником! Всем здоровья!Ура!  |
Техподдержка/общение |
TG-канал |
Max-канал |
|
| Наше приложение во VK |
|
|
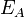 — математическое ожидание количества очков, которое наберёт игрок A в партии с B;
— математическое ожидание количества очков, которое наберёт игрок A в партии с B; — рейтинг игрока A;
— рейтинг игрока A;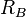 — рейтинг игрока B.
— рейтинг РёРіСЂРѕРєР° B. — коэффициент, значение которого равно 10 для сильнейших РёРіСЂРѕРєРѕРІ (рейтинг 2400 Рё выше), 15 — для РёРіСЂРѕРєРѕРІ СЃ рейтингом меньше чем 2400 Рё 30 (было 25) — для новых РёРіСЂРѕРєРѕРІ (первые 30 партий СЃ момента получения рейтинга Р¤РДЕ);
— коэффициент, значение которого равно 10 для сильнейших РёРіСЂРѕРєРѕРІ (рейтинг 2400 Рё выше), 15 — для РёРіСЂРѕРєРѕРІ СЃ рейтингом меньше чем 2400 Рё 30 (было 25) — для новых РёРіСЂРѕРєРѕРІ (первые 30 партий СЃ момента получения рейтинга Р¤РДЕ); — фактически набранное РёРіСЂРѕРєРѕРј A количество очков (1 очко Р·Р° победу, 0,5 — Р·Р° ничью Рё 0 — Р·Р° поражение);
— фактически набранное игроком A количество очков (1 очко за победу, 0,5 — за ничью и 0 — за поражение); — новый рейтинг игрока A.
— новый рейтинг РёРіСЂРѕРєР° A.
